Love and Math: The Heart of Hidden Reality - Frenkel, Edward  ## Metadata - Author: **Frenkel, Edward** - Full Title: Love and Math: The Heart of Hidden Reality - Category: #books ## Highlights -  Photo by K.G. Libbrecht ([View Highlight](https://read.readwise.io/read/01jfpgwjjthk5xdms16v8f04p3)) - *universality* . The circle group is not only the group of symmetries of a round table, but also of all other round objects, like a glass, a bottle, a column, and so forth. In fact, to say that a given object is round is the same as to say that its group of symmetries is the circle group. This is a powerful statement: we realize that we can describe an important attribute of an object (“being round”) by describing its symmetry group (the circle) ([View Highlight](https://read.readwise.io/read/01jfpgydjh3dfeqkmvr2xg146b)) - *objectivity* . The concept of a group, for example, is independent of our interpretation. It means the same thing to anyone who learns it. Of course, in order to understand it, one has to know the language in which it is expressed, that is, mathematical language. But anyone can learn this language ([View Highlight](https://read.readwise.io/read/01jfpgz1ax296srskmzcyr0fjq)) - *endurance* . There is little doubt that the Pythagorean theorem meant the same thing to the ancient Greeks as it does to us today, and there is every reason to expect that it will mean the same thing to anyone in the future. Likewise, all true mathematical statements we talk about in this book will remain true forever. ([View Highlight](https://read.readwise.io/read/01jfpgzgrkd1pba8dbg4y8hsw6)) - *relevance* of mathematics to the physical world. For example, a lot of progress has been made in quantum physics in the past fifty years because of the application of the concept of symmetry to elementary particles and interactions between them. From this point of view, a particle, such as an electron or a quark, is like a round table or a snowflake, and its behavior is very much determined by its symmetries ([View Highlight](https://read.readwise.io/read/01jfph18czjfzjsjzjj6n9yj1r)) - And the Langlands Program is a great example. I like to think of it as a Grand Unified Theory of Mathematics because it uncovers and brings into focus mysterious patterns shared by different areas of math and thus points to deep, unexpected connections between them. ([View Highlight](https://read.readwise.io/read/01jfphgv1jw1g171vf1e13xq70)) - The key point of the Langlands Program is the concept of symmetry that is already familiar to us. We have talked about symmetry in geometry: for example, any rotation is a symmetry of a round table. Our study of these symmetries has led us to the notion of a group. We then saw that groups appear in mathematics in different guises: as groups of rotations, braid groups, and so on. We have also seen that groups were instrumental in classifying elementary particles and predicting the existence of quarks. The groups that are relevant to the Langlands Program appear in the study of numbers. ([View Highlight](https://read.readwise.io/read/01jfphjx8zxz56bn7mtbzekf6q)) - To explain this, we need to talk first about the numbers that we encounter in our everyday life. Each of us was born in a particular year, lives in a house that has a particular number on the street, has a phone number, a PIN to access a bank account at the ATM, and so forth. All of these numbers have something in common: each of them is obtained by adding number 1 to itself a certain number of times: 1 + 1 is 2, 1 + 1 + 1 is 3, and so on. These are called the natural numbers. ([View Highlight](https://read.readwise.io/read/01jfphkakzq11pc9g68tg9hfhy)) - We also have the number 0, and the negative numbers: −1, −2, −3,... As we discussed in [Chapter 5](#ch5) , these numbers go by the name “integers.” So an integer is a natural number, or number 0, or the negative of a natural number. ([View Highlight](https://read.readwise.io/read/01jfphkm1ag0hgbz65nc5prbc8)) - We also encounter slightly more general numbers. A price, in dollars and cents, is often represented like this: $2.59, meaning two dollars and fifty-nine cents. This is the same as 2 plus the fraction 59/100, or 59 times 1/100. Here 1/100 means the quantity that being added to itself 100 times gives us 1. Numbers of this kind are called rational numbers, or fractions. ([View Highlight](https://read.readwise.io/read/01jfphkz6j2a9d642h9267e4hv)) - The vast majority of the numbers we encounter in our everyday life situations are these fractions, or rational numbers. But there are also numbers that are not rational. An example is the square root of 2, which we write as follows: 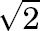 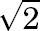. It is the number whose square is equal to 2. Geometrically, 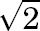 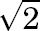is the length of the hypotenuse of the right triangle with legs of length 1. ([View Highlight](https://read.readwise.io/read/01jfphmrjgk8v3jttgxs70bbwb)) - The story of Galois is one of the most romantic and fascinating stories about mathematicians ever told. A child prodigy, he made groundbreaking discoveries very young. And then he died in a duel at the age of twenty. There are different views on what was the reason for the duel, which happened on May 31, 1832: some say there was a woman involved, and some say it was because of his political activities. Certainly, Galois was uncompromising in expressing his political views, and he managed to upset many people during his short life. ([View Highlight](https://read.readwise.io/read/01jfphsgvc840r23s6j5d05zzx))